The C2000 microcontroller, built on the C28x+FPU architecture, enhances the original C28x fixed-point CPU by adding specific registers and instructions to support IEEE single-precision floating-point operations. This makes it fully compatible with programs originally written for fixed-point processors, meaning no modifications are needed when transitioning. 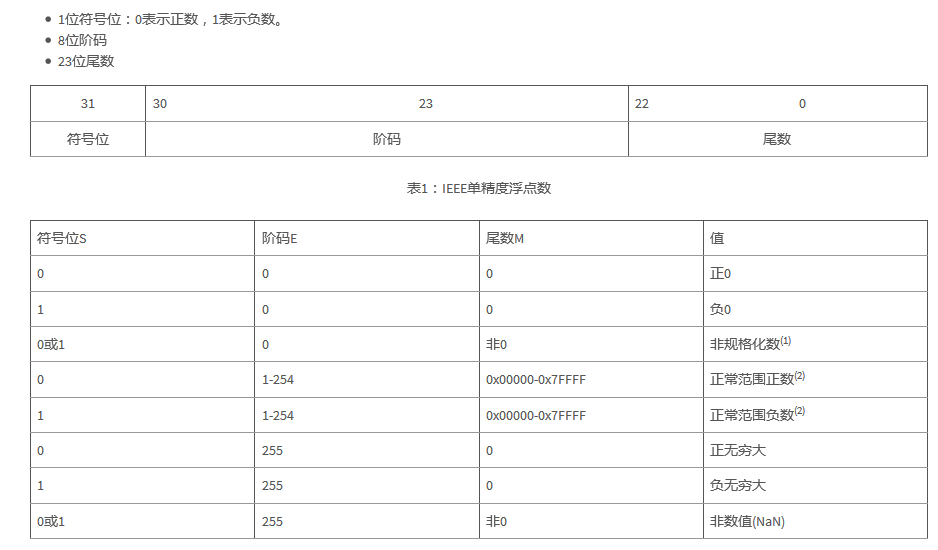Compared to fixed-point processors, floating-point C2000 devices offer several advantages: - Simplified programming - Improved performance, especially in complex algorithms like division, square root, FFT, and IIR filtering - Greater program reliability **First, IEEE 754 Single-Precision Floating Point** The C28x+FPU follows the IEEE 754 standard for single-precision floating-point numbers, which consist of a sign bit, exponent, and mantissa. The format is as shown in Table 1.

mantissa

Table 1: IEEE Single-Precision Floating-Point Numbers

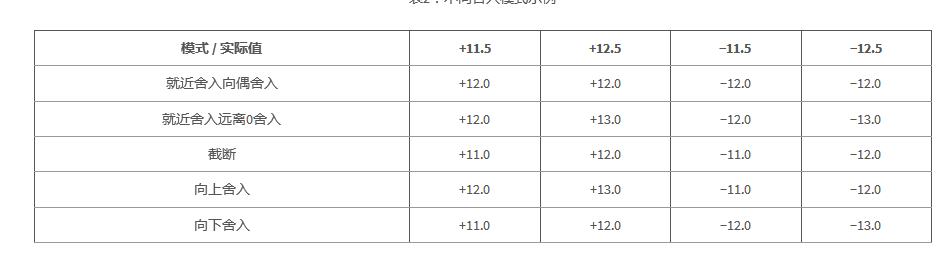
There are two main types of values: normalized and denormalized. Normalized values use the formula (-1)^s × 2^(E-127) × 1.M, while denormalized values use (-1)^s × 2^(E-126) × 0.M. The normal range covers values from approximately ±1.7 × 10^-38 to ±3.4 × 10^38. The IEEE 754 standard includes special values such as NaN (Not a Number) and infinity, along with rounding modes and arithmetic rules. However, the C2000 simplifies some aspects: - It does not differentiate between positive and negative zero - Denormalized values are treated as zero - NaN and infinity are handled similarly The C28x+FPU supports only two rounding modes: truncation and round-to-nearest-even. The latter is the default setting in the compiler, as shown in Table 2.

Table 2: Examples of Different Rounding Modes

**Second, Computing Skills and Points to Note on Floating-Point C2000 Chips** Floating-point numbers have limited precision due to the number of bits in the mantissa. While most errors are small, repeated calculations can accumulate these errors, leading to significant discrepancies. An example illustrates this: adding 11.7 to a variable 20,001 times on both the CPU and CLA of the F28379D chip results in different outputs. This discrepancy arises because the CPU uses round-to-nearest-even by default, while the CLA uses truncation. By adjusting the rounding mode using assembly code, the results can be aligned. Additionally, the error in 11.7 itself is small, but after multiple additions, the accumulated error becomes noticeable. To reduce this, defining the variable as a long double (64-bit) helps maintain higher precision. It’s important to note that the C28x CPU only supports hardware-based single-precision (32-bit) floating-point operations. Double-precision (64-bit) operations are handled via software, resulting in slower execution. The CLA also lacks support for 64-bit operations. Looking at the assembly code for float and long double variables, we see that float operations take fewer cycles compared to long double operations, highlighting the trade-off between precision and speed. **Third, Conclusion** 1. The CPU and CLA in C2000 have different default rounding modes, which can lead to varying results. Adjusting the rounding mode via code ensures consistency. 2. Repeated calculations with single-precision floats may introduce errors. Using long double improves accuracy. 3. The C28x CPU only supports hardware-based single-precision floating-point operations. Future C2000 generations will include hardware support for 64-bit double-precision arithmetic, improving performance and precision.

Wireless Keyboard Case

Bluetooth Wireless Keyboard Case,Wireless Keyboard Case with Touchpad,Wireless Keyboard Case for Tablet,Smart Wireless Keyboard Case,Universal Wireless Keyboard Case

Shenzhen Ruidian Technology CO., Ltd , https://www.wisonen.com